Zernike polynomials
Definition in polar coordinate system
The Zernike polymials form an orthogonal basis within the unit circle, when defined using polar coordinates (\(\rho,\theta\)) as follows,
where \(\theta\) measured from the \(x\) axis, \(\delta_{m,0}\) is the Kroneckers delta function, and
with the integer indices \(n\) and \(m\) that meet the conditions \(n \geq 0\), \(|m| \leq n\), and \(n-|m|\) is even, are allowed. The normalization factor, \begin{equation} N_n^m = \sqrt{\frac{2(n+1)}{1 + \delta_{m,0}}}, \end{equation} which is promoted by the Optical Society of America's document Standards for Reporting the Optical Aberrations of Eyes makes the polynomials have unit norm.
Definition in Cartesian coordinate system
The Zernike polynomials can also be expressed in Cartesian coordinates as follows (See Carpio & Malacara and section 4 in Akondi & Dubra)
where \(n'\)=(\(n\)-\(|m|\))/2.
Download code here:
- Matlab - Zernike evaluation function in polar coordinates
- Matlab - Zernike evaluation function in Cartesian coordinates
- Python - TODO function
Indexing
Here we adopt the single index notation promoted by the Optical Society of America’s document Standards for Reporting the Optical Aberrations of Eyes.
Reporting the Optical Aberrations of Eyes (SROAE) TODO: insert citation, etc. The table below shows how to convert from the two index to the SROAE one index notation.
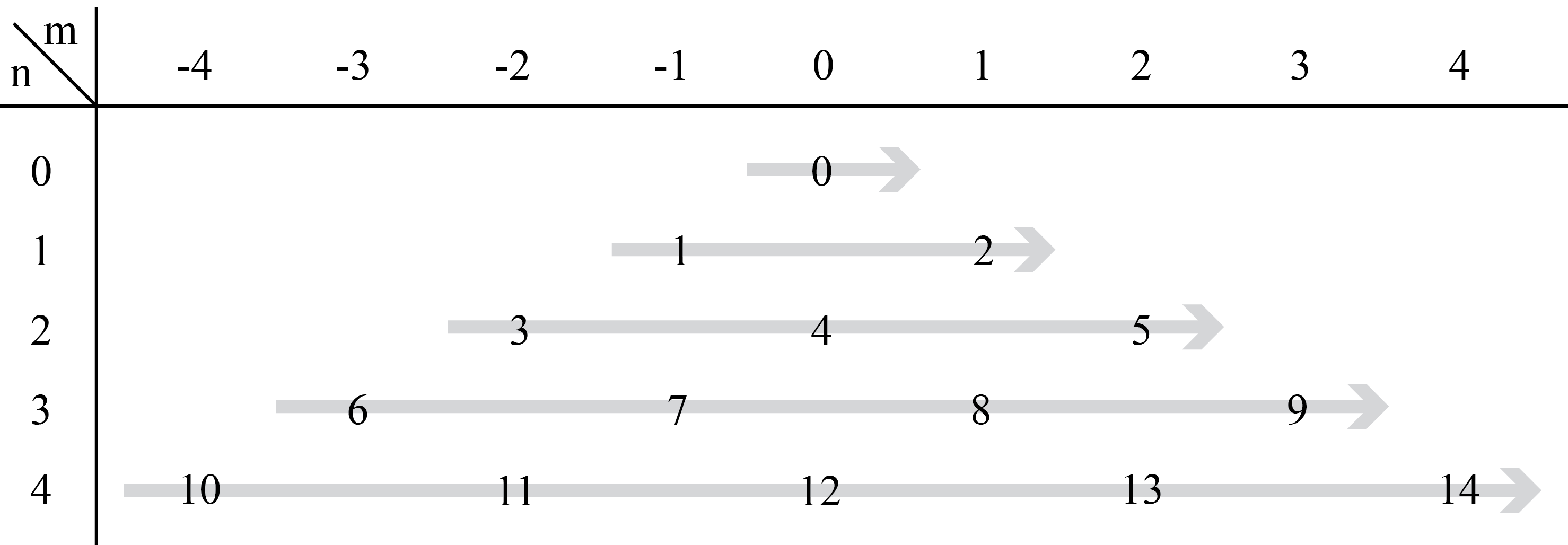
Download code here:
- Matlab - Function to convert Single index to Double index Zernike notation and vice versa
- Python - TODO function
Wavefront representation
The Zernike polynomials introduced in equation \ref{zernike_definition_B&W} form an orthonormal basis in the function space defined by the unit circle ((Omega)), that is,
This condition is written in different ways according to which normalisation factor is used when defining the polynomials. The definition given here is the one we believe more practical and is also the recommended one in the SROAE. The wavefront $W$ can be expressed in terms of the Zernike polynomials in the same way we decompose a vector in a linear space by projecting onto vectors that form an orthonormal basis (which is actually the case),
where the amplitude coefficients are given by
The norm of the wavefront in the pupil space, is the root-mean-square (RMS) of the wavefront $\sigma_W$ and takes the simple form
| \(n\) | \(m\) | \(Z_n^m(\rho,\theta)\) | \(Z_n^m(x,y)\) | |
|---|---|---|---|---|
| 0 | 0 | 1 | 1 | piston |
| 1 | -1 | \(2 \rho \sin \theta\) | \(2x\) | tip |
| 1 | -1 | \(2 \rho \sin \theta\) | \(2y\) | tilt |
| 2 | -2 | \(\sqrt{6} \rho^2 \sin ( 2 \theta )\) | \(2\sqrt{6}xy\) | astigmatism \(45^o\) |
| 2 | 0 | \(\sqrt{3} ( 2 \rho^2 -1 )\) | \(\sqrt{3} \left[2 (x^2+y^2) - 1\right]\) | defocus |
| 2 | 2 | \(\sqrt{6} \rho^2 \cos ( 2 \theta )\) | \(\sqrt{6} \left(y^2 - x^2\right)\) | astigmatism \(0^o\) |
| 3 | -3 | \(\sqrt{8} \rho^3 \sin ( 3 \theta )\) | \(\sqrt{8} \left(3xy^2-x^3\right)\) | triangular astigmatism \(x\)-axis |
| 3 | -1 | \(\sqrt{8} (3\rho^3-2\rho)\sin (3\theta)\) | \(\sqrt{8} \left(-2x+3xy^2+3x^3\right)\) | third order coma \(x\)-axis |
| 3 | 1 | \(\sqrt{8} (3\rho^3-2\rho)\cos (3\theta)\) | \(-2y+3yx^2+3y^3\) | third order coma \(y\)-axis |
| 3 | 3 | \(\sqrt{8} \rho^3 \cos ( 3 \theta )\) | \(-3yx^2+y^3\) | triangular astigmatism \(y\)-axis |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| 4 | 0 | $\sqrt{5}\left(6\rho^4 - 6\rho^2 +1\right)$ | $\sqrt{5}\left[6(x^2+y^2)^2 - 6(x^2+y^2)+1\right]$ | spherical aberration |
Conversion to diopters
In ophthalmology and optometry the spectacle prescription is made in terms of sphere, cylinder and cylinder angle for practical reasons related to the lens manufacture. These three numbers can be expressed in terms of the second order Zernike terms, i.e.defocus and the two astigs. The power of a lens with spherical surfaces can be defined as the inverse of its focal length, and the unit to express it is called diopter ($D = m^{-1}$) and referred to as \textit{sphere} (not to be confused with spherical).
If we for example look at the human eye, that has a typical focal length of $17mm$, the corresponding sphere value is about $60D$. The minimum step between ophthalmic lenses is $1/8D$ although in practice optometrist will only prescribe using a minimum step of $1/4D$.
The other corrective type of lens used in spectacles is the cylindrical lens, that is a lens with spherical section in one direction and flat in the perpendicular one. Again, its power will be given in diopters.
The power $\Phi_A$ of a cylinder can be calculated in terms of the Zernike amplitude coefficients \cite{LIA94} as
where D is the diameter of the pupil. The axis of that cylinder is given by
and
The sphere is calculated as
where the introduction of half the amplitude of the cylinder can be thought of in terms of making the value $\Phi_D$ the focal length of the spherical lens that would correct best both defocus and astigmatism simultaneously.\
Download code here:
- Matlab - focal shift calculator function
- Matlab - script demonstrating its use
- Python - focal shift calculator function
- Python - script demonstrating its use